Fuzzy Temperature Fault Tolerance

A paper demonstrating that drifting between temperatures 1 and 2, ultimately remaining in 2, in the 2HAM can prevent certain assembly errors.

Abstract

We consider the problem of fault-tolerance in nanoscale algorithmic self-assembly. We employ a standard variant of Winfree’s abstract Tile Assembly Model (aTAM), the two-handed aTAM, in which square “tiles” – a model of molecules constructed from DNA for the purpose of engineering self-assembled nanostructures – aggregate according to specific binding sites of varying strengths, and in which large aggregations of tiles may attach to each other, in contrast to the seeded aTAM, in which tiles aggregate one at a time to a single specially-designated “seed” assembly. We focus on a major cause of errors in tile-based self-assembly: that of unintended growth due to “weak” strength-1 bonds, which if allowed to persist, may be stabilized by subsequent attachment of neighboring tiles in the sense that at least energy 2 is now required to break apart the resulting assembly; i.e., the errant assembly is stable at temperature 2. We study a common self-assembly benchmark problem, that of assembling an n×n square using O(logn) unique tile types, under the two-handed model of self-assembly. Our main result achieves a much stronger notion of fault-tolerance than those achieved previously. Arbitrary strength-1 growth is allowed; however, any assembly that grows sufficiently to become stable at temperature 2 is guaranteed to assemble into the correct final assembly of an n×n square. In other words, errors due to insufficient attachment, which is the cause of errors studied in earlier papers on fault-tolerance, are prevented absolutely in our main construction, rather than only with high probability and for sufficiently small structures, as in previous fault-tolerance studies. We term this the fuzzy temperature model of faults, due to the following equivalent characterization: the temperature is normally 2, but may drift down to 1, allowing unintended temperature-1 growth for an arbitrary period of time. Our construction ensures that this unin-tended growth cannot lead to permanent errors, so long as the temperature is eventually raised back to 2. Thus, our construction overcomes a major cause of errors, insufficient strength-1 attachments becoming stabilized by subsequent growth, without requiring the detachment of strength-2 bonds that slows down previous constructions, and without requiring the careful fine-tuning of thermodynamic parameters to balance forward and reverse rates of reaction necessary in earlier work on fault-tolerance. Although we focus on the task of assembling an n×n square, our construction uses a number of geometric motifs and synchronization primitives that will likely prove useful in other theoretical (and, we hope, experimental) applications

Overview

The kTAM was introduced alongside the aTAM as a model that more accurate reflects laboratory conditions by allowing for rates of attachment and detachment relative to the temperature of the simulation. This allowed for error, and work in the kTAM has largely focused on methods of reducing or eliminating these errors. One of the foremost methods of error reduction is proofreading, wherein many errors must compound in order to stabilize in the structure. Proofreading has been shown to arbitrarily reduce error.

This paper concerns itself with an alternative approach to error-handling in laboratory work by simulating changes in temperature in the 2HAM. The 2HAM being another variant on the aTAM that, rather than allow attachment and detachment, allows the combination of any two subassemblies, which is another attempt to more closely mimic laboratory conditions. By changing the temperature from 1 to 2 and back again before ultimately settling at temperature 2 erroneous growth can be entirely prevented rather than merely made improbable. This shifting of temperature is dubbed the fuzzy temperature model. This paper demonstrates two constructions in this model and defines the model itself.

Informal Definition of Fuzzy Temperature Model

The fuzzy temperature assembly model permits rampant temperature τ = 1 growth of supertiles under the two-handed assembly model. We are then interested in what producible temperature τ = 1 assemblies become stable at temperature τ = 2. If even a single temperature τ = 1 assembly becomes stable at temperature τ = 2 and is inconsistent with what can be built in a purely temperature τ = 2 assembly model, the system is deemed error prone. On the other hand, if all temperature τ = 1 assemblies that are stable at temperature τ = 2 have a valid temperature τ = 2path of growth to a supertile that is producible under a pure temperature τ = 2 model, then the system is deemed fuzzy temperature fault-tolerant. Put another way, even with arbitrary erroneous strength 1 attachments, a fuzzy temperature fault-tolerant system guarantees that such errors cannot stabilize at temperature 2 unless the stabilized supertile can itself grow into a correct temperature τ = 2 assembly, which means such an assembly is not really an error.

Results

The first construction is of a 2HAM binary counter with \(O(\log n)\) tile types. The construction uses a combination of geometric hindrance and nondeterminism to ensure growth towards the one unique supertile. The tileset and final construction are shown below.

The tile set which grows a 4-bit binary counter.

The counter grown by the preceding tile set.

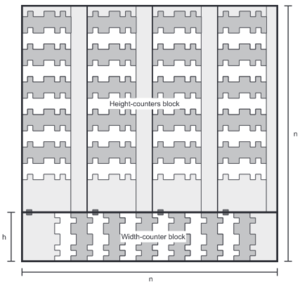
The second construction is an n x n square with \(O(\log n)\) tile types using similar ideas of geometric interference, nondeterminism, and in this case fuzzy fault tolerance.

Simplified diagram of the n x n square.

Future Work

One possible improvement on the square construction is a reduction to the aTAM optimal \(O(\frac{\log n}{\log \log n})\) tile types, or a proof that such a reduction is impossible. Other avenues of study include the assembly time of the square construction and increasing the 'connectedness' of the square since the current terminal supertile is relatively 'floppy.'